近期，北京航空航天大学中法工程师学院师生在湍流模型稳定性分析方面取得重要进展。研究团队深入探究了经典k-ε湍流模型在Kolmogorov流中的不动点稳定性问题，揭示了该模型在周期边界条件下无法收敛至正确物理解现象的数学本质。这一成果为深入理解RANS模型的计算局限性、改进工业湍流模拟策略提供了新的理论视角。相关研究成果以“Stability of k-ε model in Kolmogorov flow”为题，发表于JCR Q1期刊《Applied Mathematics and Mechanics (English Edition)》。北京航空航天大学中法工程师学院硕士毕业生郭佳硕为论文第一作者，方乐教授为通讯作者。

雷诺平均纳维-斯托克斯（RANS）方法是工程中进行流场预测和湍流模拟的主流手段，其中两方程k-ε模型因其形式简单而应用广泛。然而，该模型在强旋流、逆压梯度流等复杂流动中精度受限，且其迭代求解过程可能收敛于非物理的不动点解。以往研究多集中于模型的经验修正与应用验证，对其内在非线性动力学系统在相空间中的演化机制和稳定性，以及其与边界条件的关系缺乏系统认识。

Kolmogorov流作为一种经典的周期受力剪切流，具有解析形式的平均速度剖面，为湍流模型的机理研究提供了理想的理论与数值实验平台（图1）。

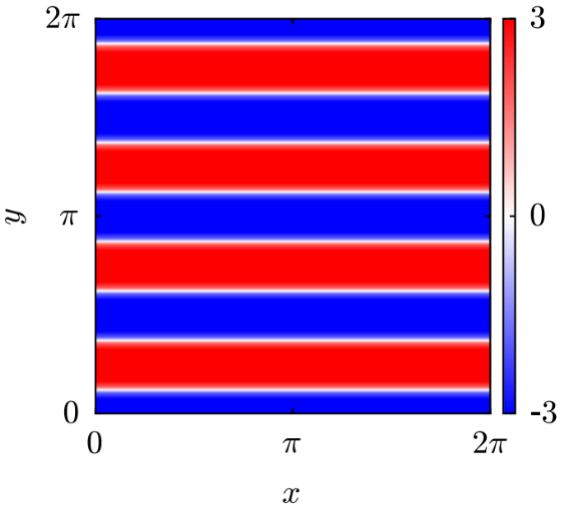
(a)Kolmogorov流稳态解

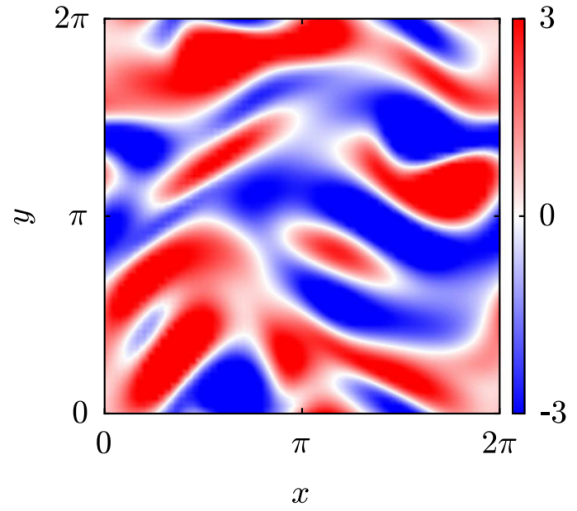
(b)瞬态Kolmogorov流

图1 Kolmogorov流动速度场，Re=40

研究团队结合理论分析与直接数值模拟（DNS）数据，将k-ε模型方程在Kolmogorov流中简化为一维系统。研究首先发现，在周期性边界条件下，k-ε模型仅存在唯一的平凡不动点（零解），并且RANS迭代计算可能收敛于该不稳定的非物理解（图2）。

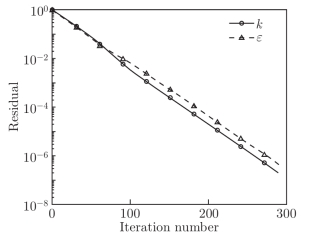
图2 方程残差收敛曲线，结果均收敛至平凡解

研究发现，在演化过程中，湍动能（k）与耗散率（ε）的零波数模态逐渐主导，因此构建空间均匀性假设。通过时空积分与谱分析，研究揭示了模型相空间中存在的渐近线结构（图3，图4）。

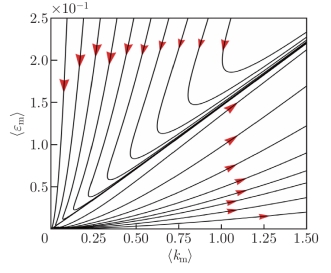
图3 相空间演化轨迹与渐近线

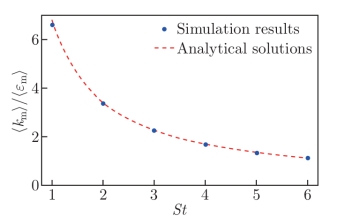
图4 相空间理论渐近线斜率与数值结果对比

基于均匀性假设，研究团队从两个层面系统分析了模型的稳定性：一是相轨迹相对于渐近线的收敛特性；二是渐近线上不动点沿渐近线方向的演化稳定性。通过李雅普诺夫线性稳定性分析，推导出了由模型参数（

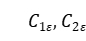）决定的稳定性相图（图5，图6）。该相图将参数空间划分为三个特征区域，分别对应渐近线与不动点均稳定、均不稳定、以及渐近线稳定但不动点不稳定的不同动力学机制。

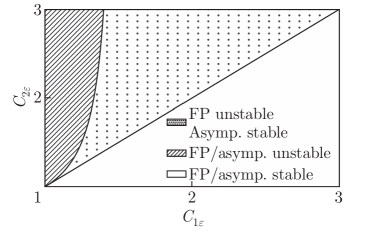
图5 Kolmogorov流周期性边界参数稳定性相图

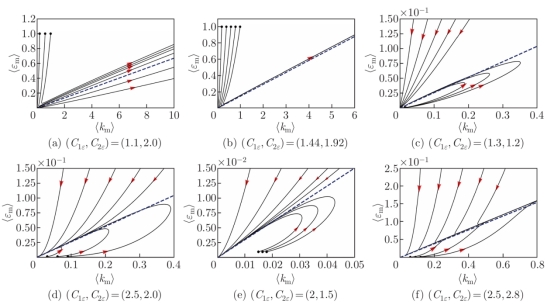
图6 Kolmogorov流相空间轨迹验证（虚线为理论渐近线）

研究进一步对比了周期性边界与固定边界条件的影响。结果表明，在固定边界条件下，k-ε模型能够收敛到一个稳定的非平凡不动点，但其数值强烈依赖于边界值的设定（图7）。这从数学上解释了为何建议对k-ε模型使用固定值或零梯度边界条件，而非周期性边界条件。

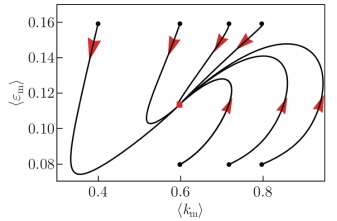
图7 Kolmogorov流固定边界条件不同初始条件的相空间演化轨迹

为验证上述理论结论，团队利用开源计算流体力学软件OpenFOAM进行了系统的数值计算。通过在周期和固定边界条件下选取代表性参数点进行计算，获得的相轨迹演化与理论预测高度一致。此外，在一个更贴近工程实际的槽道流案例中进行的耦合RANS计算也表明，即使在动量方程与湍流模型方程耦合迭代的情况下，周期边界条件依然会导致收敛困难，而固定边界条件则能引导模型收敛至更合理的流场结果（图8，图9）。

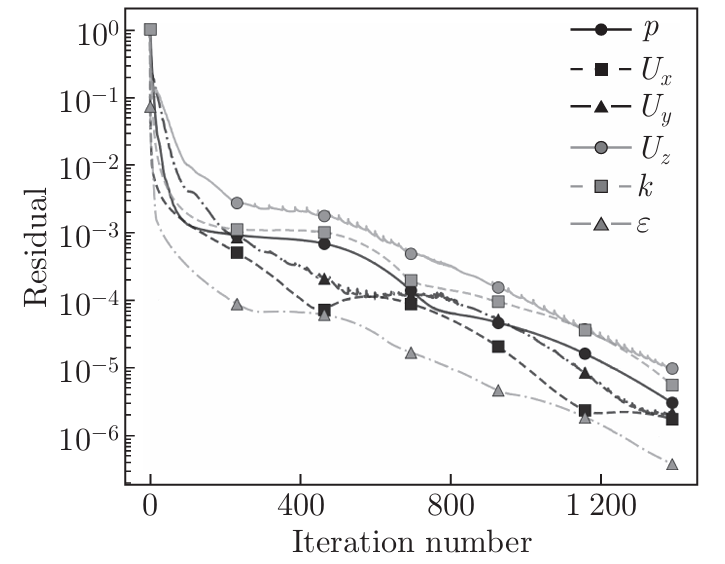
（a）固定边界条件收敛曲线

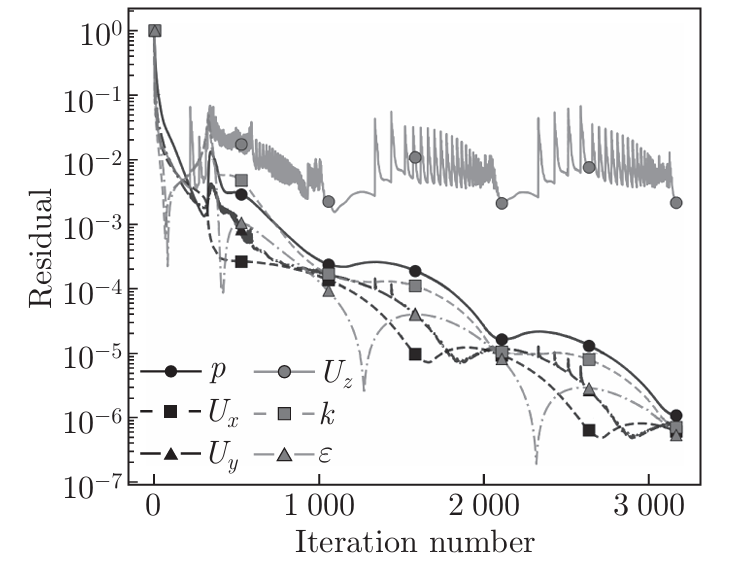
（b）固定边界条件收敛曲线

图8  三维槽道算例中不同边界条件下的收敛曲线对比

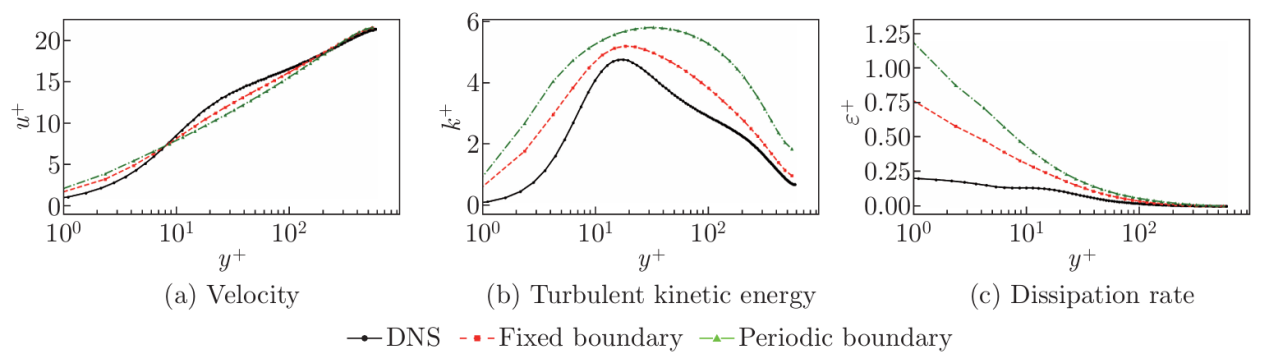
图9 三维槽道算例中不同边界条件计算结果对比

该研究首次系统阐释了k-ε模型在Kolmogorov流相空间中的渐近线结构与稳定性机理，明确了边界条件设置对模型收敛性的决定性影响。所建立的基于相空间渐近线的稳定性分析框架，为深入理解湍流模型的非线性动力学行为、规避非物理解、以及发展更稳健的RANS模拟策略奠定了理论基础，对提升航空航天发动机内流、飞行器绕流等工程问题的模拟预测能力具有重要指导意义。

本项研究工作得到了国家自然科学基金（Nos. 12372214、 U2341231）的资助。

文章链接：https://www.amm.shu.edu.cn/EN/10.1007/s10483-026-3337-8